Software that accompanies my books:
Facility Location Software – SITATION
Updated software to accompany NETWORK AND DISCRETE LOCATION: MODELS, ALGORITHMS AND APPLICATIONS for Windows 95 and above.
The SITATION software as well as the other programs that accompany Daskin’s text (Network and Discrete Location: Models, Algorithms, and Applications) have been updated to run under Windows 95.
The following enhancements have been made to the original version of the program:
- The programs are entirely menu-driven and run under Windows 95 and later versions of Windows.
- SITATION now solves five classes of location problems including: P-median, P-center, Set Covering, Maximal Covering, and Uncapacitated Fixed Charge Problems.
- SITATION includes branch and bound capabilities to allow the user to obtain very tight (usually provably optimal) solutions.
- Additional mapping capabilities have been added to SITATION.
- SITATION allows the user to zoom in on portions of the tradeoff curves and maps.
- SITATION allows the user to specify alphanumeric (text-based) node names.
- SITATION solves the Covering-Median tradeoff problem using the weighting method. (See section 8.2 of my book)
- The newest version of SITATION will solve problems with up to 300 nodes and the program does not expire!
To learn more about the software, click (for a PDF document about the software).
The latest version of this software is available by clicking here
You will receive a zipped file that is about 7 MB long.
The file contains the zipped version of four programs and another 13 data files.
Documentation is available here
Note that there were minor errors with earlier versions
You should download the current version which I hope is bug free.
Spreadsheet for the Traveling Salesman Problem
You can download an EXCEL© spreadsheet that allows you to try your hand at solving a 49-node traveling salesman problem. You have to list the two character state abbreviation for the 48 capitals in the continental United States plus Washington, DC in an order to solve the traveling salesman problem. The spreadsheet will automatically compute the (great circle) distance between each pair of cities as well as the total distance of the tour. The spreadsheet will also provide error messages if a state abbreviation is spelled incorrectly and/or if a state is used more than once. Finally, the spreadsheet includes a map showing the outline of the United States as well as the tour that you have identified.
Have fun with it.
Click here to download a Zip file that contains this spreadsheet.
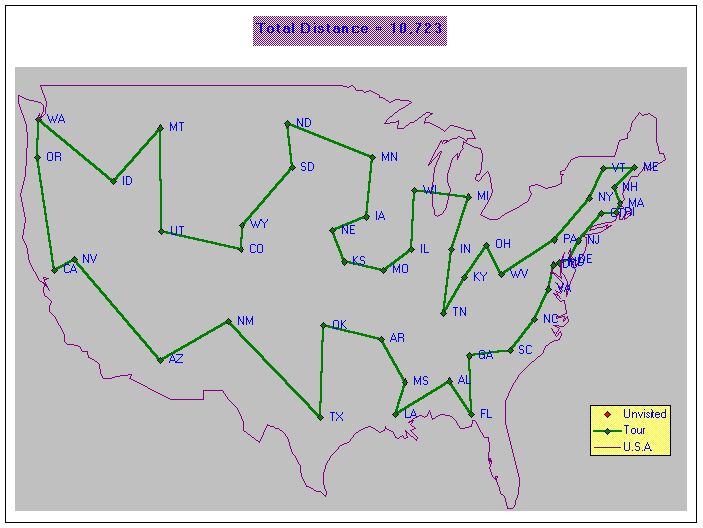
Here is a good (but NOT the best) solution…
Spreadsheet for Facility Location Problems
You can download an EXCEL© spreadsheet that allows you to try your hand at solving a variety of facility location problems on a 49-node dataset. The dataset corresponds to the capitals of the 48 states in the continental United States plus Washington, D.C. The spreadsheet is pre-loaded with the 1990 state populations as demands and initial fixed costs. You can change these numbers as you see fit.
The problems that you can try to solve include Maximal Covering, P-Median, and Uncapacitated Fixed Charge location problems. For each problem, you can locate as many facilities as you want. To locate a facility, you simply specify the two character state abbreviation for the capital of the state. The spreadsheet provides error messages in the event you spell a state abbreviation incorrectly or in the event that you list a location twice. The spreadsheet will automatically compute the objective function values for the three problems identified above and will show the results in a spreadsheet as well as on a dynamically updated map built into the spreadsheet.
Have fun with it.
Click here to download a Zip file that contains this spreadsheet.
Time Dependent Queueing Analyzer
This program allows you to explore the differences between steady-state and time-dependent queueing problems. The model uses a sinusoidal pattern for the mean of a Poisson arrival process. The problem you are faced with is that of determining the starting time and shift duration for full time and part time employees to attain various objectives. The program solves for the steady-state state probabilities (assuming they exist) at each instant of time. The program also solves the Chapman-Kolmogorov first-order differential equations for the time-dependent state probabilities and reports such measures as the time-dependent number in the system and the time-dependent probability of waiting for service.
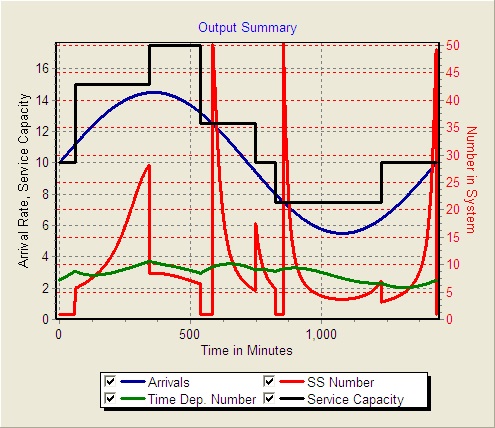
The figure below shows the mean arrival rate (in blue), the number on duty (in black) , the steady-state expected number in the system (in red) and the time-dependent expected number in the system in green. Note that the number on duty can be less than the number needed for steady state (for short periods of time). During these times, the expected number in the system in steady state is reported as 0, since the number is not defined.
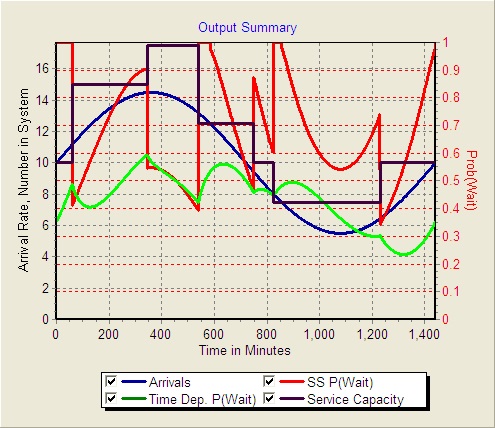
The graph below shows the steady-state (red) and time-dependent (green) probability of waiting for service. Again, if the steady-state conditions do not exist at a particular instant in time, the probability of waiting is reported as 1 (as is the case for times before time 60. For times between 0 and 60, 5 serves are needed and only 4 are available.
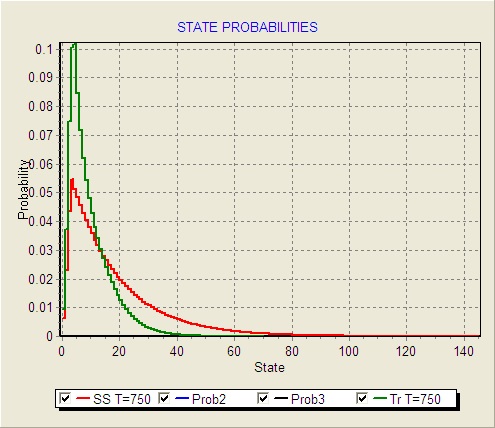
The figure below shows the distribution of the number in the system in steady-state (red) and in the time-dependent (green) cases at time 750. Note that the distributions are quite different and that the mean of the number in the system at time 750 assuming steady state operation is quite a bit larger than is the mean accounting for the time-dependent nature of the arrival and service processes.
Click here to download a zipped file containing this program.
Click here to download a PDF version of a Powerpoint presentation explaining this program in greater detail.
